1. 直管元件(jian)在內壓作用下(xia)的應力(li)分(fen)布

   通常將直管元件劃分不銹(xiu)鋼厚(hou)壁管和薄壁不銹鋼管，根據不同的假設理論來研究直管元件的應力分布。不(bu)銹鋼(gang)厚壁管和不銹鋼薄壁管的劃分一般以k=do/di=1.2為界，當h＞1.2時為厚壁管，h≤1.2時為薄壁不銹鋼管。

2. 厚(hou)壁管的應力分布(bu)

   假設直管(guan)(guan)的(de)內(nei)(nei)、外徑分別為di和do，沿壁厚任意點(dian)到(dao)管(guan)(guan)中(zhong)心(xin)的(de)距離為p，管(guan)(guan)道承受均勻的(de)介質內(nei)(nei)壓為p，那(nei)么厚壁管(guan)(guan)中(zhong)各點(dian)的(de)應力計算表達式如下：

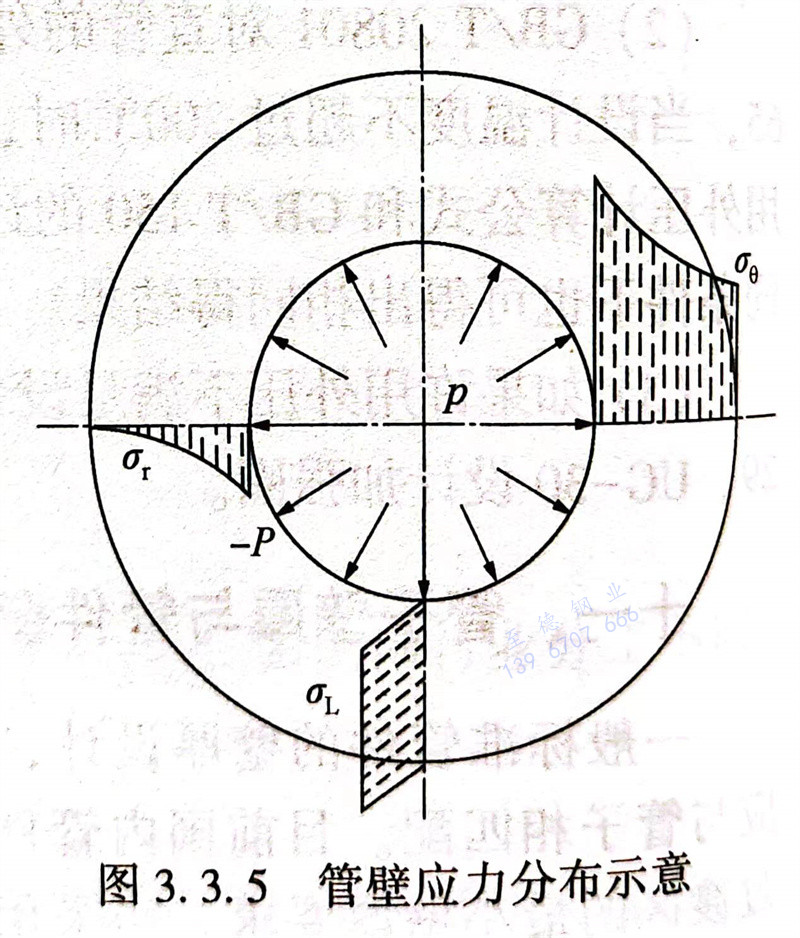
從上述公式可看(kan)出以(yi)下(xia)規律：①. 軸向應力σL沿管(guan)道(dao)壁厚均勻分(fen)布；周向應力σ，和徑向應力σr 沿管(guan)道(dao)壁厚分(fen)布是不均勻的(de)。各(ge)應力沿管(guan)壁厚的(de)分(fen)布示意圖(tu)，見圖(tu)3.3.5。

                                          ②. 周(zhou)向應力σ在內壁處(chu)最大，在外壁處(chu)最小；

                                          ③. 徑向應(ying)力σr，在(zai)內(nei)壁(bi)處為(wei)-p，在(zai)外壁(bi)處為(wei)0。

                                          ④. 三個(ge)應(ying)(ying)力(li)分量(liang)中，數值上周向應(ying)(ying)力(li)最(zui)大，軸向應(ying)(ying)力(li)σL次之，徑(jing)向應(ying)(ying)力(li)σr最(zui)小。

3. 薄壁(bi)管的應(ying)力分布(bu)

  對于薄(bo)壁管，在(zai)理論上有以下假設：

   ①. 由于管壁(bi)很(hen)薄，認(ren)為(wei)應力沿管壁(bi)是均勻(yun)分(fen)布的(de)。

   ②. 對于(yu)薄(bo)壁不(bu)銹鋼管，徑(jing)向(xiang)應力相對于(yu)周向(xiang)應力和(he)軸向(xiang)應力很小，可以忽(hu)略不(bu)計。

  ③. 根據上述假(jia)設，由材料力學可知，內壓作(zuo)用下薄壁不銹(xiu)鋼(gang)管的應(ying)力計算表(biao)達(da)式如下：

 可見，在內壓作用下，薄壁不銹鋼管的周向(xiang)(xiang)應力是軸向(xiang)(xiang)應力的2倍(bei)，且(qie)大于0；徑向(xiang)(xiang)應力為0。